How Transformers Echo Control Theory

Transformer models have captivated a lot of AI research in most of the past decade, and in this post my goal is to make them seem more interesting to controls people, who have much to contribute to the field. I will be making gross generalizations to draw such entry points. At least, I found transformer models more interesting after finding a few parallels in dynamical systems & controls ¹. This post attempts to explore those parallels.

Large Language Models (LLMs) are used almost everywhere, and for everything, but a notable property that enables this utility is their ability to learn in-context. That is, from a sequence (of letters) $${x_1,x_2,...,x_N}$$, they learn to try to predict the next few terms of the sequence $${x_{N+1},...x_{N+l}}$$. This is possible in case of language processing using contextual token embeddings and dealing with tokens, instead of arbitrary words. In-context tokenization, by the way, is also how the statistical treatment of natural language processing is different now as compared to before the existence of transformers (think bag-of-words, WordPiece, byte-pairs, etc.). Transformers achieve this by the key property of attention. We don’t need to know the exact equations, but attention’s properties. Since attention is permutation invariant (technically, it is equivariant under permutation – the output permutes in the same order as the input), transformers also need positional encoding.

The Embeddings are a transformation $$z_k = E(x_k)$$, into some higher dimensional space, and positional encoding is arithmetically added to get $$\tilde{z}_k=z_k + p_k$$. Since it utilizes subword tokens and token embedding matrices to come up with an attention metric that we can treat as a nonlinear embedding $$Y=\mathrm{nonlinear}(\{x_{-1}, x_{-2}, ...,x_{-d}\})$$. This simplification may seem like it insists upon itself, but we will see shortly that it helps transformers to be applicable beyond language tasks. After some manipulation with the attention metric, transformers attempt to directly let self-attention be learned in a way such that each token directly decides what other tokens matter by treating token sequences as a set of tokens & positions. So $$q_k = Q\tilde{z}_k$$, $$\kappa_k=K\tilde{z}_k$$, and $$v_k=V\tilde{z}_k$$. are projections to form nonlinear attention equation: $$\mathrm{attention}=\mathrm{softmax}\left(\frac {QK} {c_k} \right)V$$. In some sense,

• $$q_k$$ is the state asking what do I need?
• $$k_k$$ is a different state broadcasting what it has to offer, and
• softmax is an adaptive nonlinear coupling among them. Matrices $$Q,K,V$$ help project the vectors appropriately. Before this, recurrent neural networks passed information step-by-step, attention directly connects each state to each other state.

We can see such a tiny transformer in action.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class  MultiHeadSelfAttention(nn.Module):
   def  __init__(self, d_model, n_heads):
   	super().__init__()
   	assert d_model % n_heads == 0
   	self.d_model = d_model
   	self.n_heads = n_heads
   	self.d_k = d_model // n_heads
   	#combine QKV as one linear for efficiency; split later
   	self.w_q = nn.Linear(d_model, d_model, bias=False)
   	self.w_k = nn.Linear(d_model, d_model, bias=False)
   	self.w_v = nn.Linear(d_model, d_model, bias=False)
   	self.w_out = nn.Linear(d_model, d_model, bias=False)

   def  forward(self, x, mask=None):
   	#x: (batch, seq_len, d_model)
   	B, T, _ = x.shape
   	Q = self.w_q(x).view(B, T,  self.n_heads,  self.d_k).transpose(1,2)  # (B, heads, T, d_k)
   	K = self.w_k(x).view(B, T,  self.n_heads,  self.d_k).transpose(1,2)
   	V = self.w_v(x).view(B, T,  self.n_heads,  self.d_k).transpose(1,2)
   	#scaled dot-product
   	scores = (Q @ K.transpose(-2,-1)) / math.sqrt(self.d_k)  # (B, heads, T, T)
   	if mask is  not  None:
   	scores = scores.masked_fill(mask == 0,  float('-inf'))
   	att = F.softmax(scores, dim=-1)  # (B, heads, T, T)
   	out = att @ V # (B, heads, T, d_k)
   	out = out.transpose(1,2).contiguous().view(B, T,  self.d_model)  # (B, T, d_model)
   	
   	return  self.w_out(out), att # return attention weights too

along with the computation of the projection matrices to compute attention. The complete code can be found here ². The sequence to train is simply the sentence hello world. , and attempts to predict the next 25 characters after the input ‘he’ as follows:

1
2
3
4
5
6
7
8
9

Epoch 1/8 avg_loss = 0.5890 
Epoch 2/8 avg_loss = 0.0527 
Epoch 3/8 avg_loss = 0.0406 
Epoch 4/8 avg_loss = 0.0368 
Epoch 5/8 avg_loss = 0.0349 
Epoch 6/8 avg_loss = 0.0338 
Epoch 7/8 avg_loss = 0.0333 
Epoch 8/8 avg_loss = 0.0327 
Generated: hello world. hello world. h

Essentially, transformers have a way to compute $$x_{k+1}=f(x_k)$$, taking into account entire trajectory $$Y$$ via attention mechanism. Wait, that looks suspiciously like system identification $$\rightarrow$$ prediction!! This is no coincidence. And here is the crux of the article—transformers are great at sequence-to-sequence modeling; therefore, they are also good at direct sequence learning that often arises in controls problems. In fact, the encoder (a multi-headed self-attention mechanism that is aware of the entire ’trajectory’ or context) and decoder (masked self-attention that generates the sequence one token at a time and cannot look into the future) in the transformer learn the contextual representation of the entire input, and the predicted auto-regressive output, respectively.

If you thought you were going to see an application of the same to trajectory prediction or system identification, you are spot on! Now we delve into the often-seen control system application with a simple toy example. Consider a simple dynamical model of a car (Dubins car model). Suppose the dynamics in 2D evolve autonomously as per some unknown dynamics $$x_{k+1}=f(x_k)$$,and we are given a number of past trajectories evolving under the dynamics. The task at hand is to find the next $$l$$ positions given the input sequence positions given the input sequence $$Y$$, where dynamics $$f$$ are unknown.

Below is the predicted trajectory, as learned by our tiny transformer. Again, the complete code to reproduce can be found here ².

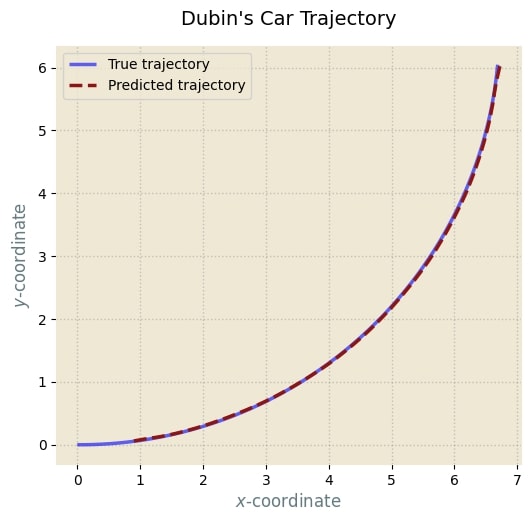
This has been a very standard (non-trivial) problem of system identification and/or prediction, which a simple Kalman Filter can solve for linear systems (and an extended Kalman Filter for nonlinear systems). There are more nuanced methods such as Koopman Operator-based projections to higher-dimensional spaces. Curiously, just like the $$\mathcal{O}(n^2)$$ growth of transformer complexity with sequence length, such methods also grow quadratically, as they too take into account cross-dependency using Gramian structures.

Clearly, transformer self-attention is very closely related to state-space modeling commonly used in control systems. So it should be no surprise that there are state-space methods that are now finding use, and in some cases replacing transformer models :) ^{3 4}

Perhaps that is a teaser for another post on state-space models to follow! Meanwhile, a much better introduction to transformers from scratch can be found here ⁵.

> Written with StackEdit.